Mondriaan for sparse matrix partitioning
Mondriaan partitioner
Mondriaan is a sequential program written in C
that can be used to partition a rectangular sparse
matrix, an input vector, and an output vector
for parallel sparse matrix-vector multiplication.
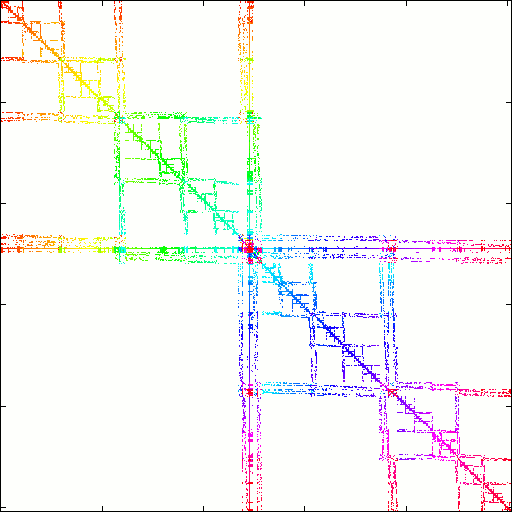
The program is based on a recursive bipartitioning
algorithm that cuts the matrix horizontally and vertically,
in a manner resembling some of the famous Mondriaan paintings.
The algorithm is multilevel, hypergraph-based, and two-dimensional.
It reduces the amount of communication and it spreads both computation
and communication evenly over the processors.
The program can partition hypergraphs with integer vertex weights
and uniform hyperedge costs,
but it is primarily intended as a matrix partitioner.
Download
Download the latest version of the
Mondriaan software, version 4.2.1 (tar gzipped),
released August 8, 2019.
The user's guide and MATLAB documentation can be found here.
 The latest development version of the Mondriaan software can be found in
the git
repository.
The latest development version of the Mondriaan software can be found in
the git
repository.
Optimal partitoning
Database of optimally partitioned matrices using the MondriaanOpt program.
Under development.
Slides of related lecture, Sparse Days at St. Girons, June 30, 2015.
The user's guide for MondriaanOpt can be found here.
Bug fix in version
4.2.1 (August 8, 2019)
This version fixes a bug when using a non-default option in version 4.2:
if a 1D partitioning is chosen by Splitstrategy=onedimrow or onedimcol,
and CheckUpperBound=yes this may cause the CheckUpperBound function
to create a 2D partitioning instead of 1D in rare cases
(when the communication volume is high). In such a case for rectangular matrices
it would create a partitioning with volume (max(m,n)+1)(P-1),
instead of the volume (min(m,n)+1)(P-1) that could have been achieved.
Thanks to Steven Fleuren and Femke van Ieperen for discovering this bug.
Furthermore, this version removes some harmless compiler warnings
and improves bad behaviour by the Makefile, which forgot to remove
one file (testHelper_DisconnectedMatrix.o) when cleaning up.
New features of version
4.2 (September 14, 2017)
Version 4.2 contains several improvements compared to version 4.1.
These are:
- A zero-volume search based on finding connected components is performed before every
bipartitioning, to perform easy splits quickly if they exist.
- Improved load balance by moving free nonzeros (in a row and column that are both cut) after every bipartitioning.
- Overall speed improvements.
- A separate MondriaanStats program which is able to quickly determine the communication volume
and other information about a computed partitioning.
New features of version
4.1 (November 7, 2016)
Version 4.1 contains several improvements compared to version 4.0.
These are:
- The MondriaanOpt program, which offers a way to solve the
bipartitioning problem to optimality.
The MondriaanOpt program is available as stand-alone program, as Matlab
routine and as linkable archive.
- MondriaanPlot can now also generate SVG (Scalable Vector Graphics)
images of partitionings.
- Some bugfixes and fixes for some compiler warnings, as well as
updates to the user's manual.
New features of version 4.0 (August 29, 2013)
Version 4.0 contains several improvements compared to version 3.11.
These are:
-
The medium-grain partitioning method, which offers both improved quality and faster partitioning compared to the localbest (pure Mondriaan) method.
Medium-grain is also the new default partitioning strategy.
-
More advanced matching of hypergraph vertices in the coarsening phase of the partitioning, through the use of a better matching algorithm (PGA'), which is guaranteed to generate matchings that have at least half the weight of the heaviest possible matching.
-
Support for a new hypergraph cost metric which measures the communication volume of all-neighbor communication: the lambda*(lambda - 1)-metric.
-
Improved quality through iterative refinement of bipartitionings via medium-grain.
New features of version 3.11 (December 15, 2010)
Version 3.11 contains several improvements compared to version 3.0.
These are:
-
The
Extended Matrix-Market (EMM) output format
enables the storage of many matrix-like objects in a single file. In the case of Mondriaan, this potentially decreases the number of output files from 5 or more for partitioning a single matrix, to a single file. (By no means is the EMM format tied to Mondriaan: the format can easily and portably be used to share more complex matrix/vector-formulated problems.) Since it remains close to the original Matrix-Market format, existing parsers are envisioned to be adapted with minimal effort.
-
The hierarchy of the separator blocks is now included in the output,
for all permutation strategies, i.e. Separated Block Diagonal (SBD) and (reverse) Bordered Block Diagonal (BBD).
This enables building a full binary tree out of the SBD and BBD structures.
-
Mondriaan can now force symmetric permutations, that is, generate PAP^T for general A. In particular, Mondriaan is now able to retain the symmetry of symmetric input matrices.
-
The symmetric finegrain splitting strategy. This represents a symmetric sparse matrix A using half the number of vertices and hyperedges, compared to the regular finegrain method. This significantly improves partitioning time for symmetric input matrices, albeit at the cost of some loss in quality, when compared to finegrain.
-
The Matlab interface now makes more Mondriaan output available to the users. This enables easy direct application, e.g. to reduce the
fill-in in LU-type methods and to accelerate cache-sensitive computations. See also the revised
User's guide for Mondriaan's Matlab interface.
Minor update version 3.01 (August 3, 2010)
This update repairs a small bug with ordering to Bordered Block Diagonal (BBD)
form.
New features of version 3.0 (July 27, 2010)
Version 3 contains many improvements compared to version 2.
These are:
- New algorithms for matrix ordering into Separated Block Diagonal (SBD)
form suitable for cache-oblivious sparse matrix-vector multiplication, and also into
Bordered Block Diagonal (BBD) form suitable for
and sparse LU decomposition.
- Better quality of the matrix partitioning, in particular for fine-grain partitioing.
- Hypergraph partitioning by the cut-net metrics, as well as the common (lambda-1)-metric.
- Matlab (TM) interface. Sparse matrices can be partitioned within the Matlab environment.
- PaToH interface. Mondriaan can now also use PaToH as a hypergraph bipartitioner,
instead of its native bipartitioner.
- Visualisation of the partitioning process, by the MondriaanPlot and MondriaanMovie programs.
- Mondriaan has now been made a separate library which can easily be intergrated into existing
applications.
- The package has been tested on a variety of operating systems
including Linux, Mac OS X, and a variety of architectures, including
X86_64, Apple Mac, IBM BlueGene/L, and others.
- The User's guide.
has been extended and includes a simple example program that shows how to use Mondriaan as a library.
There is also a separate User's guide for Mondriaan's Matlab interface
minor bug-fix version 2.01 (June 9, 2009)
Alexander Gusak from the Belarusian State University,
Faculty of Applied Mathematics and Computer Science,
found and fixed a few errors: a memory leak,
an opened file which was not closed, and an
an uninitialised string terminator.
He also suggested a few improvements
to prevent overflow for huge sparse
matrices. These allowed him to partition matrices of 6 million rows
and columns and 400 million nonzeros.
New features of version 2.0 (July 14, 2008)
Version 2 contains many improvements compared to version 1 (released May 10, 2002).
These are:
- New algorithms for vector partitioning, which often achieve the best
communication load balance for the given matrix partitioning.
- Much faster partitioning, by a factor of 10; this improvement was
already incorporated in the minor release v1.02 from 2005.
- Better quality of the matrix partitioning. On average, communication volume
is reduced by 10%, mainly due to scaling of the inner products of matrix columns
in the coarsening phase.
- Inclusion of the finegrain partitioning method (proposed by Catalyurek and Aykanat 2001).
- Inclusion of a hybrid between the original Mondriaan method and
the finegrain method.
- Some new hypergraph partitioning capabilities. Mondriaan 2.0 can handle hypergraphs
with arbitrary integer vertex weights, but only with uniform hyperedge costs.
- Can also handle non-powers of two for the number of processors.
- Full documentation of every function. (Total 96 functions.)
- A unit test for every function.
- Package has been tested on Linux, Mac OS X, Solaris, and using Valgrind
for finding memory leaks.
- User's guide.
- More liberal license: GNU Lesser General Public License
One bug fix compared to version 1.02:
versions 1.X contained a small memory leak, discovered by Albert-Jan Yzelman using Valgrind.
It was fixed by adding statements: free (C[nc]1.Start); free (C[nc]1.Match)
inside the uncoarsening loop of function RunMLGraphPart in file HKLFM.c.
You may have run out of memory earlier than needed when using version 1.02.
Now you can solve larger problems!
Minor update version 1.02 (March 7, 2005)
Changes the data structure used in the inner product matching
of the coarsening. This makes the software about 10 times faster.
Thanks to Umit Catalyurek who pointed out an inefficiency
in my previous version. This concerns function FindMatchIM
in file HKLFM.c.
Another change is that the (non-default) option of weighted edges is removed.
This option was inferior to the default option
and hence should not be used anyway.
Note that to use V1.02 you must discard the old file mondriaan.defaults.
Mondriaan will then automatically create a new default file.
Minor update version 1.01 (December 17, 2003)
Makes comments ANSI-C compliant, delimiting them by /* ... */.
Fixes the following two bugs.
-
May 31, 2002. Wouter Meesen: For compiling on a Windows system
with the visual c++ compiler, you have to remove all the words 'inline'
from the source code. This word occurs in the files:
DistributeVec.h, GainBucket.c, GainBucket.h, HKLFM.c, HKLFM.h.
Same remark holds for Cray T3E compiler CC (Joris Koster, May 2002).
-
Sept. 2, 2003. A remark by a sharp-eyed anonymous referee of our paper
led us to reexamine the conversion from a sparse symmetric matrix
to the full version in the function SparseMatrixSymmetric2Full
from the file SparseMatrix.c.
This function contains an error affecting the first nonzero.
The error only occurs for symmetric matrices stored in symmetric input format.
Thanks to the referee!
Initial release Mondriaan version 1.0 (May 10, 2002)
Related papers
The original Mondriaan algorithm and implementation has been published in
"A Two-Dimensional Data Distribution Method
for Parallel Sparse Matrix-Vector Multiplication",
by Brendan Vastenhouw and Rob H. Bisseling,
SIAM Review, 47, No. 1 (2005) pp. 67-95.
The new vector partitioning algorithms and implementations have been published in
"Communication balancing in parallel
sparse matrix-vector multiplication",
by Rob H. Bisseling and Wouter Meesen,
Electronic Transactions on Numerical Analysis,
21 (2005) pp. 47-65,
special issue on Combinatorial Scientific Computing.
The new matrix ordering algorithms and implementations have been published in
Cache-oblivious sparse matrix-vector multiplication
by using sparse matrix partitioning methods by Albert-Jan N. Yzelman
and Rob H. Bisseling,
SIAM Journal on Scientific Computing,
31, No. 4 (2009) pp. 3128-3154.
An extension to 2D is given in
Two-dimensional cache-oblivious sparse matrix-vector multiplication
by A. N. Yzelman and Rob H. Bisseling,
Parallel Computing, 37, No. 12 (2011) pp. 806-819.
The hybrid between the original Mondriaan method and
the finegrain method has been published as a book chapter
Two-Dimensional Approaches to Sparse Matrix Partitioning
by Rob H. Bisseling, Bas O. Fagginger Auer, A. N. Yzelman, Tristan van Leeuwen and Ümit V. Çatalyürek,
Chapter 12 of Combinatorial Scientific Computing, Chapman and Hall/CRC, pp. 321-349 (2012).
The lambda*(lambda - 1)-metric is introduced in
A new metric enabling an exact hypergraph model for the communication volume in distributed-memory parallel applications
by O. Fortmeier, H. M. Bücker, B. O. Fagginger Auer, R. H. Bisseling, Parallel Computing, 39, No. 8 (2013) pp. 319-335.
The medium-grain method is described in
A medium-grain method for fast 2D bipartitioning of sparse matrices by
D. M. Pelt and R. H. Bisseling,
Proceedings IEEE International Parallel & Distributed Processing Symposium 2014,
IEEE Press, pp. 529-539.
An exact algorithm for obtaining an optimal partitioning of small matrices for 2 processors is given in
An
exact algorithm for sparse matrix bipartitioning,
by Daniel M. Pelt and Rob H. Bisseling,
Journal of Parallel and Distributed Computing, 85 (2015) pp. 79-90.
Postprint version.
The corresponding program MondriaanOpt has been included in Mondriaan version 4.1.
The zero-volume search and the load balance improvement by moving free nonzeros
(and some other improvements)
introduced in version 4.2 are described in the MSc thesis of Marco van Oort,
Accelerating the Mondriaan sparse matrix partitioning package,
Utrecht University, May 2017.
Extensive background reading on the parallel sparse matrix-vector
multiplication problem, including a detailed discussion of the Mondriaan algorithm,
can be found in Chapter 4 (pp. 163-250) of
 Parallel Scientific Computation: A Structured Approach using BSP and MPI,
by Rob H. Bisseling,
Oxford University Press,
March 2004. 324 pages. ISBN 978-0-19-852939-2.
OUP home page of the book.
Parallel Scientific Computation: A Structured Approach using BSP and MPI,
by Rob H. Bisseling,
Oxford University Press,
March 2004. 324 pages. ISBN 978-0-19-852939-2.
OUP home page of the book.
Trailer
Trailer announcing Mondriaan version 2 by Sarai Bisseling
(Quicktime movie, 11.6 MB).
Selected related lectures by Rob Bisseling
-
CECAM Workshop Open Source Software for Microscopic Calculations,
June 19-21, 2002, Lyon, France:
Mondriaan,
partitioning software for sparse matrix computations
(24 transparancies, 719kB, PDF format, generated using Prosper)
-
A hybrid 2D method for sparse matrix partitioning
by Rob Bisseling,
Tristan van Leeuwen,
and Umit Catalyurek.
Lecture at
SIAM Conference on Parallel Processing for Scientific Computing
San Francisco, February 22-24, 2006.
(29 transparancies, 612kB, PDF format).
-
Sparse matrix partitioning, ordering, and visualisation
by Rob Bisseling, Albert-Jan Yzelman, and Bas Fagginger Auer.
Lecture at
Parallel Matrix Algorithms and Applications, Basel, Switzerland,
June 29 - July 2, 2010.
Copyright
This software is copyrighted (2002, 2008, 2010, 2013, 2016, 2017) by
Rob Bisseling, Bas Fagginger Auer,
Tristan van Leeuwen, Wouter Meesen, Marco van Oort, Daan Pelt, Brendan Vastenhouw, Albert-Jan Yzelman.
You can use and modify it under the
GNU Lesser General Public License,
see GNU Licenses.
Also see the files, README, COPYING, COPYING.LESSER.
Anything free, as usual, comes with no guarantee!
Contributions
Besides the authors mentioned in the copyright notice,
others have contributed as well:
- Umit Catalyurek: interface to finegrain partitioning, PaToH
- Ken Stanley: visualisation
Other contributions are welcome!
Test matrices
Most matrices we use in our tests can be obtained from
Tim Davis'
University of Florida Sparse Matrix Collection.
The term-by-document matrices used in the SIAM Review paper are:
tbdmatlab.mtx
(430171 nonzeros, 3.2 Mbyte) and
tbdlinux.mtx
(2157675 nonzeros, 18.9 Mbyte), both in gzip-compressed Matrix Market format.
The RSA matrices used in the paper
"Mondriaan sparse matrix partitioning for attacking cryptosystems
by a parallel block Lanczos algorithm - a case study"
by Rob H. Bisseling and Ildiko Flesch,
Parallel Computing
32 Nr. 7/8 (2006) pp. 551-567,
Final preprint (Sept 2006),
are:
rsa_c82.mtx
(16338 rows, 16307 columns, 507716 nonzeros) and
rsa_c98.mtx
56274 rows, 56243 columns, 2075889 nonzeros).
Note that the paper uses the transposed of the matrices given here.
The matrices are courtesy of Richard Brent.
Last updated August 19, 2019.
to
Home page Rob Bisseling.
 Parallel Scientific Computation: A Structured Approach using BSP and MPI,
by Rob H. Bisseling,
Oxford University Press,
March 2004. 324 pages. ISBN 978-0-19-852939-2.
OUP home page of the book.
Parallel Scientific Computation: A Structured Approach using BSP and MPI,
by Rob H. Bisseling,
Oxford University Press,
March 2004. 324 pages. ISBN 978-0-19-852939-2.
OUP home page of the book.
 The latest development version of the Mondriaan software can be found in
the git
repository.
The latest development version of the Mondriaan software can be found in
the git
repository.
 Parallel Scientific Computation: A Structured Approach using BSP and MPI,
by Rob H. Bisseling,
Oxford University Press,
March 2004. 324 pages. ISBN 978-0-19-852939-2.
OUP home page of the book.
Parallel Scientific Computation: A Structured Approach using BSP and MPI,
by Rob H. Bisseling,
Oxford University Press,
March 2004. 324 pages. ISBN 978-0-19-852939-2.
OUP home page of the book.