Rekenstaafjes van Napier en de Abacus
Rekenstaafjes van Napier
Uitgevonden door: John Napier
Jaar: 1617
De rekenstaafjes van napier zijn een hulpmiddel voor vermenigvuldiging en deling. Zelfs worteltrekken en machtsverheffen behoren tot de mogelijkheden.

Ik zal uitleggen hoe een vermenigvuldiging teruggebracht kan worden tot een simpele optelling. Op elk staafje is de vermenigvuldigingstafel te zien van de getalen 0 t/m 9.
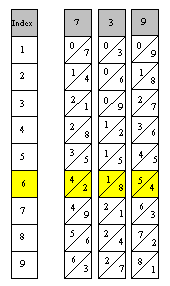
De vermenigvuldiging van 6 x 5 kan gedaan worden met het staafje met daarop de tafel van 5 en daar te kijken in de 6e rij. Het nummer van een rij kan aangegeven worden met een index-staafje (in het plaatje links te zien).
Vermenigvuldigingen met getallen (1 t/m 9, neem bijv. 6) met grote getallen (bijv. 739) kunnen gemakkelijk uitgevoerd worden met de staafjes 7,3 en 9 naast elkaar gelegd en het index-staafje links er naast gelegd. De rij van indexgetal 6 geeft de uitkomst van 6 x 739 als de eenheden, tien-, honderd- en duizendtallen worden opgeteld.
6 x 7 = 4 2 (6 x 700)
6 x 3 = 1 8 (6 x 30)
6 x 9 = 5 4 (6 x 9)
-----------------
6 x 739 = 4 4 3 4
| | | |
| | | +- eenheden
| | +--- tientallen
| +----- honderdtallen
+------- duizendtallen
Met de "/"-teken op de staafjes kun je zien welke getallen bij elkaar moeten worden opgeteld.
Abacus

Een abacus bestaat uit een rechthoekig raamwerk met daarbinnen een aantal staven of draden. Een horizontale balk deelt deze staven (of draden) in twee ongelijke delen. Om de staven zitten een soort kralen. Bij het bovenste (kleinste) gedeelte 2 om elke staaf, bij het onderste gedeelte 5 stuks. Het geheel is een soort numeriek stelsel, waarin elke staaf een soort decimaal positie aangeeft, zoals ook in onze "arabische" notatie. Er is op de staven meer ruimte dan dat de kralen nodig hebben, die zo vrij op en neer geschoven kunnen worden, van of naar de horizontale balk toe. De plaats van de kralen op een bepaalde staaf representeert een getal op de respectievelijke decimale positie.
Optellen
85607 + 439 = 86046
- Stel de abacus op "nul" door alle kralen weg te schuiven van de horizontale balk.
- Stel het getal 85607 in. De zeven in de meest rechtse kolom; de nul in de tweede kolom; de 6 in de derde; de 5 in de vierde en de 8 in de vijfde kolom van rechts. De zeven moet ingesteld worden door één kraal in het bovenste gedeelte en twee kralen in het oderste gedeelte naar de horizontale balk te schuiven. De kraal in het bovenste gedeelte heeft de waarde 5 en de twee kralen in het onderste gedeelte hebbende waarde 1+1=2. Samen is dat dus 7. Het getal 6 in de derde kolommoet dusgemaakt worden door 5 + 1, en het getal 8 door 5 + 1+1+1 (Eén kraal in het bovenste gedeelte en drie in het onderste)
- Het optellen van het getal 439 wordt gesplitst in een optelling van 9, 30 en 400.
- We tellen eerst 9 erbij in de rechtse kolom. 9 Kan gesplitst worden in 5 + 1+1+1+1. Eerst wordt er 5 opgeteld in het bovenste gedeelte. Als dat gedaan is, staat in de rechtse kolom het getal 12 (5+5 + 1+1). dat is meer dan 9 en daarom treken we in deze kolom er 10 vanaf (door de kralen 5+5 naar boven te schuiven) en telen we in de tweede kolom er 1 (is dus 10) bij op door 1 kraal naar de horizontale balk te schuiven. Dan moet in de rechtse kolom nog 1+1+1+1 opgeteld worden, door in het onderste gedeelte 4 kralen naar boven te schuiven. Echter na 3 kralen zijn ze op, en kan de laatste kraal niet erbj worden geteld. Dan moet er in het bovenste gedeelte 1 kraal (waarde 5) naar beneden geschoven worden en kunnen ook de 5 onderste kralen naar beneden geschoven worden.Tenslotte moet er dan weer 1 kraal naar boven geschoven worden. Vn de abacus kan dan het getal 85607 + 9 = 85616 worden afgelezen.
- Nu moet er 30 worden opgeteldinde tweede kolom van rechts. In dit geval kunnen er in het onderste gedeelte 3 kralen naar boven toe verschoven worden.
- Als laatste moet er in de derde kolom van rechts 400 worden opgeteld. Verschuif 4 kralen in het onderste gedeelte naar boven. Dan is het totaal in deze kolom 10 (eigenlijk 1000). Dat mag niet en er moet dan in de volgende kolom (vierde van rechts) in het onderste gedeelte één kraal naar boven verschoven worden. De derde kolom van rechts moet dannatuurlijk wel op nul gesteld worden, door alle kralen van de horizontale balk af te schuiven.
- Nu kan de uitkomst van 85607 + 439 worden afgelezen: 86046.
Dit lijkt vrij ingewikkeld, maar iemand die veel ervarig heeft met een abacus kan hier zeer snel mee rekenen!!
Vermenigvuldigen
Om een voorbeeld te geven van een vermenigvuldiging moeten eerst voor het gemak de staafjes genummerd worden. De meest rechtse krijgt nummer 1, de tweede van rechts nummer 2 enz. De meest linkse krijgt zo nummer 13.
Opmerking: Om met een abacus te kunnen vermenigvuldigen moet de gebruiker de tafeltjes van 1 t/m 10 kennen!
Het voorbeeld: 58 * 43 = 2494
- Stel de abacus op nul in door alle kralen weg te schuiven van de horizontale balk.
- Stel het getal 58 in, op de staven 13 en 12.
- Stel het getal 43 in, op de staven 10 en 9.
- Start de vermenigvldiging met 8 * 43. Deze berekening kan geslitst worden in 8 * 3 = 24 en 8 * 4(0) = 32(0) . Stel de uitkomst van 8 * 3 = 24 in, op de staven 2 en 1. De uitkomst van 8 * 4 = 32 kan daarbij opgeteld worden, middels de staven 3 en 2. De vermenigvulding met 8 is nu klaar en kan staaf 12 op nul gesteld worden
- dan kunnen we vermenigvuldigen met 5(0): 5(0) * 43. Deze vermenigvuldiging kan wederom opgesplitst worden 5(0) * 3 =15(0) en 5(0) * 4(0) = 20(00). De uitkomst van 5 * 3 = 15 moet worden opgeteld, op staaf 3 and 2 en de uitkomst van 5 * 4 = 20 moet worden opgeteld, op staaf 4 and 3. Staaf 13, 10 en 9 kunnen op nul gesteld worden.
- De uitkomst (2494) kan afgelezen worden op staaf 4 t/m 1.
Terug


