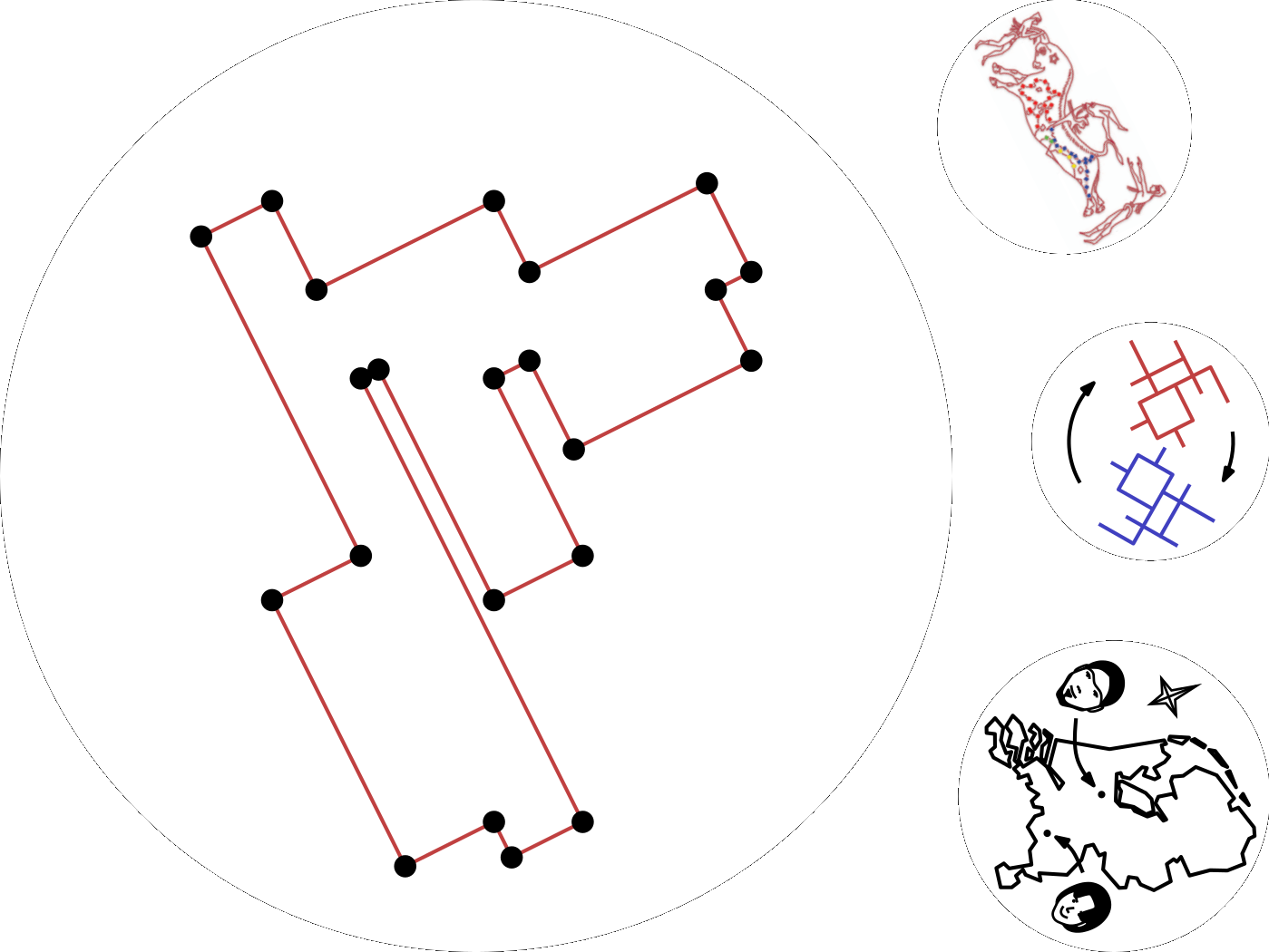
Connected Rectilinear Graphs on Point Sets
Let V be a set of n points in Rd. We study the question whether there exists an orientation such that V is the vertex set of a connected rectilinear graph in that orientation. A graph is rectilinear if its edges are straight line segments in d pairwise perpendicular directions. We prove that at most one such orientation can be possible, up to trivial rotations of 90 degrees around some axis. In addition, we present an algorithm for computing this orientation (if it exists) in O(nd) time when d is at least 2.
keywords: Computational Geometry, Graph Drawing, Graphs Theory
Journal Article (peer-reviewed)
Elena Mumford, Maarten Löffler
Connected Rectilinear Graphs on Point Sets
Journal of Computational Geometry
2, 1, 1–15, 2011
Conference Proceedings (peer-reviewed)
Elena Mumford, Maarten Löffler
Connected Rectilinear Graphs on Point Sets
Proc. 16th Symposium on Graph Drawing
LNCS 5417, 313–318, 2009
Workshop or Poster (weakly reviewed)
Elena Mumford, Maarten Löffler
Rotating Rectilinear Polygons
Proc. 17th Fall Workshop on Computational Geometry
85–86, 2007
Technical Report (not reviewed)
Elena Mumford, Maarten Löffler
Connected Rectilinear Graphs on Point Sets
UU-CS-2008-028, 2008
back to list