slides
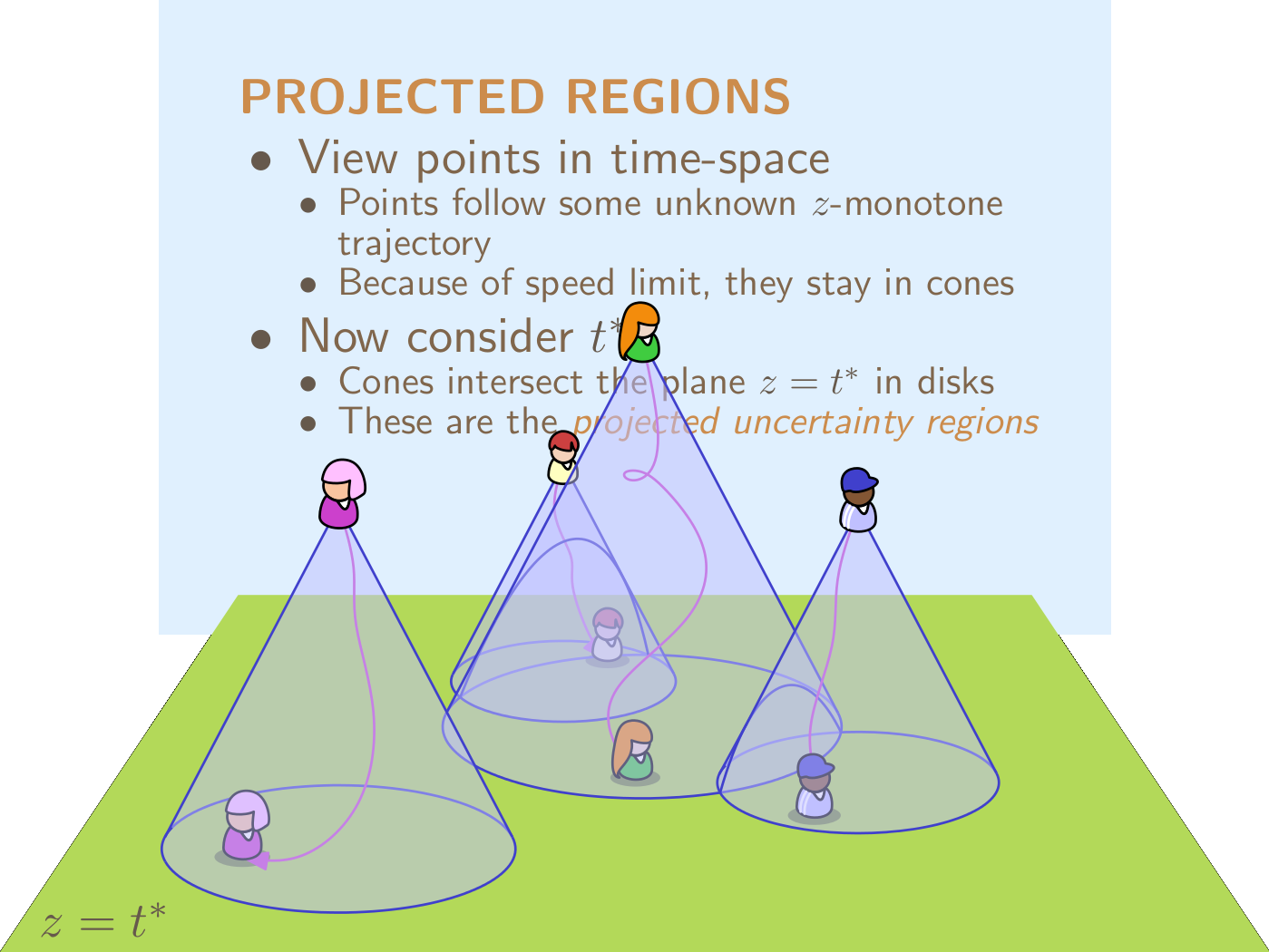
We study the problem of maintaining the locations of a collection of n entities that are moving with some fixed upper bound on their speed. We assume a setting where we may query the current location of entities, but handling this query takes a certain unit of time, during which we cannot query any other entities. In this model, we can never know the exact locations of all entities at any one time. Instead, we maintain a representation of the potential locations of all entities. We measure the quality of this representation by its ply: the maximum number of entities that could potentially be at the same location.
Since the ply could be large for every query strategy, we analyse the performance of our algorithms in a competitive framework: we consider the worst case ratio of the ply achieved by our algorithms to the intrinsic ply (the smallest ply achievable by any algorithm, even one that knows in advance the full trajectories of all entities). We show that, if our goal is to mimimise the ply at some number τ of time units in the future, an O(1)-competitive algorithm exists, provided τ is sufficiently large. If τ is small and the n entities move in any constant dimension d, our algorithm is O((ℓ/τ + 1)d − d/(d + 1))-competitive, where ℓ is the average time since the last query over all entities. We also provide matching lower bounds, and we show that computing the intrinsic ply exactly is NP-hard, even when the trajectories are known in advance.