19 January 2012
Utrecht University, David de Wiedgebouw M2.01 (see map below)
Send an email to Frank Staals (f < dot > staals < at > uu < dot > nl ) stating name and affiliation. Current list of participants.
| Time | Speaker | Title |
|---|---|---|
| 10:00–10:30 | Coffee | |
| 10:30–10:50 | Heinrich Kruger | Geometry and Grasping [abstract] |
| 10:50–11:10 | Gustavo Adolfo Ken Arroyo Ohori | Higher-dimensional object modelling in GIS based on G-maps [abstract] |
| 11:10–11:30 | Anne Driemel | Jaywalking the Dog – Computing the Frechet distance with Shortcuts [abstract] |
| 11:30–11:50 | Mathijs Wintraecken | On the Asymptotic Approximation of Manifolds Embedded in Euclidean Space [abstract] |
| 11:50–13:00 | Lunch | |
| 13:00–13:50 | Martin Nöllenburg | Labeling in Dynamic Maps [abstract] |
| (invited speaker) | ||
| 13:50–14:10 | Mini break | |
| 14:10–14:30 | Wouter van Toll | An Exact Navigation Mesh for Multi-Layered Environments [abstract] |
| 14:30–14:50 | Peter van Oosterom | A true vario-scale structure for spatial information [abstract] |
| 14:50–15:10 | Wouter Meulemans | A New Method for Subdivision Simplification with Applications to Urban-Area Generalization [abstract] |
| 15:10–15:40 | Coffee break | |
| 15:40–16:00 | Mark de Berg | |
| 16:00–16:20 | Thijs van Lankveld | On the shape of a set of points and lines in the plane [abstract] |
| 16:20–16:40 | Jean Cardinal | The Clique Problem in Ray Intersection Graphs [abstract] |
| 16:40–17:00 | Maarten Löffler | Tracking Moving Objects with Few Handovers [abstract] |
| 17:00–17:20 | Frank Staals | A splitting line model for directional relations [abstract] |
| 17:30–18:00 | Go to Hemingway | |
| 18:00- | Dinner at Hemingway |

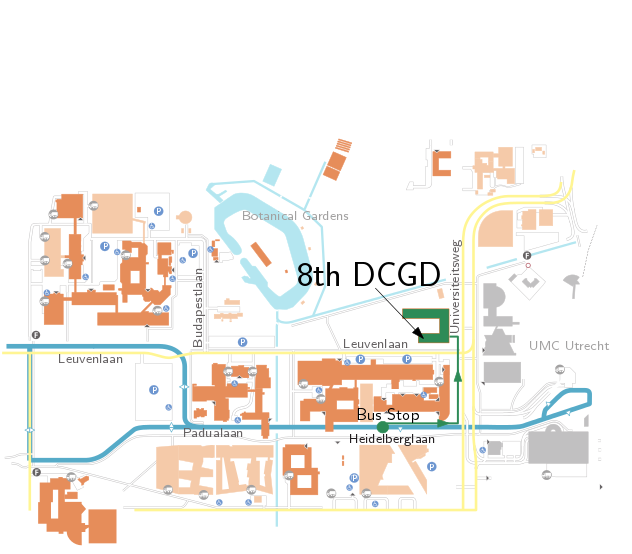
Take bus 11 or 12 and exit at the ``Heidelberglaan’’. Then walk to the David de Wiedgebouw as shown on the Map.
The David de Wiedgebouw is located on ``De Uithof’’. The address is:
David de Wiedgebouw
Universiteitsweg 99
3584 CG Utrecht
The following people have confirmed they will attend the dutch computational geometry day. If you are not listed here but you would like to attend please send an email to (f < dot > staals < at > uu < dot > nl) stating name and affiliation.
Map labeling is an important task in cartography that strongly influences the quality of a map. In the 1990s the craftsmanship of manual label placement was challenged by more and more computational approaches for automatically labeling static maps. In the last decade, another major change in cartography and geovisualization took place. Dynamic maps have become ubiquitous, e.g., in car navigation systems or location-based services on mobile devices. In this talk I will point out the new challenges for map labeling posed by dynamic maps and sketch a few recent results that address dynamic map labeling.
Real-world phenomena have traditionally been modelled in a GIS in two and three dimensions. However, we can gain new insights and improve consistency by integrating additional non-spatial dimensions, such as time, scale and attributes. While the integration of different dimensions into a higher-dimensional (hyper)cube is theoretically sound, its implementation is problematic due to several reasons. Among them, the data models and data structures used in the GIS world are not appropriate. We are therefore investigating possible data models and data structures to represent higher-dimensional GIS datasets.
In this presentation, I will explain the specific needs of GIS data in this regard, and give a sample of the problems we encounter when modelling higher dimensional objects in GIS. For this, I will present a small case study using G-maps, a data model/structure originally developed in computer graphics, but with very interesting properties.
Detailed geometric models of the real world are in increasing demand. LiDAR data is appropriate to reconstruct urban models. In urban scenes, the individual surfaces can be reconstructed and connected to form the scene geometry. There are various methods for reconstructing the free-form shape of a point sample on a single surface. However, these methods do not take the context of the surface into account. We present the guided α-shape: an extension of the well known α-shape that uses lines (guides) to indicate preferred locations for the boundary of the shape. The guided α-shape uses (parts of) these lines as boundary where the points suggest that this is appropriate. We prove that the guided α-shape can be constructed in O((n + m) log(n + m)) time, from an input of n points and m guides. We apply guided α-shapes to urban reconstruction from LiDAR, where neighboring surfaces can be connected conveniently along their intersection lines into adjacent surfaces of a 3D model. We analyze guided α-shapes of both synthetic and real data and show they are consistently better than α-shapes for this application.
In robotic grasp synthesis, we are given a geometric model of an object and asked to compute contact positions for a robotic hand to grasp the object. The contacts must be chosen such that the hand is capable of applying contact forces necessary to perform some given task. This task might be to resist some particular external force, some set of external forces, or any possible external force. In this talk I will show how this grasp synthesis problem can be reduced to a coloured geometric intersection searching problem.
We study the online problem of assigning a moving point to a base-station region that contains it. For instance, the moving object could represent a cellular phone and the base station could represent the coverage zones of cell towers. Our goal is to minimize the number of handovers that occur when the point moves outside its assigned region and must be assigned to a new region. We study this problem in terms of competitive analysis and we measure the competitive ratio of our algorithms as a function of the ply of the system of regions, that is, the maximum number of regions that cover any single point. In the offline version of this problem, when object motions are known in advance, a simple greedy strategy suffices to determine an optimal assignment of objects to base stations, with as few handovers as possible. For the online version of this problem for moving points in one dimension, we present a deterministic algorithm that achieves a competitive ratio of O(log ply) with respect to the optimal algorithm, and we show that no better ratio is possible. For two or more dimensions, we present a randomized online algorithm that achieves a competitive ratio of O(log ply) with respect to the optimal algorithm, and a deterministic algorithm that achieves a competitive ratio of O(ply); again, we show that no better ratio is possible.
The similarity of two polygonal curves can be measured using the Frechet distance. We introduce the notion of a more robust Frechet distance, where one is allowed to shortcut between vertices of one of the curves. This is a natural approach for handling noise, in particular batched outliers. We compute a constant factor approximation to the minimum Frechet distance over all possible such shortcuts. Our algorithm runs in O(c^2 k n log^3 n) time if one is allowed to take at most k shortcuts and the input curves are c-packed. For the case where the number of shortcuts is unrestricted, we describe an algorithm which runs in O(c^2 n log^3 n) time. To facilitate the new algorithm we develop several new data-structures, which we believe to be of independent interest: (i) for range reporting on a curve, and (ii) for preprocessing a curve to answer queries for the Frechet distance between a subcurve and a line segment.
When approximating a given surface in three dimensional space, let’s say an animation figure, by a triangulation we have to balance to conflicting goals. Firstly we want our approximation to be good, that is close to the original surface with respect to some metric (in this case the Hausdorff metric, which we shall define). Secondly because of finite memory and calculating power of computers we can only use a limited number of vertices to approximate the surface. We investigate (in some asymptotic sense) the optimal ratio between the Hausdorff distance and the number of vertices.
We shall discuss the following: -Hausdorff distance and curvature of surfaces in Euclidean space -Approximating convex surfaces by inscribed polyhedra (we review the work of Fejes Tóth and fill some gaps), state some result regarding the general approximation of convex surfaces. -The generalization to the approximation of convex surfaces where the vertices lie in the ambient space. -We discuss existing upper bounds on the complexity of approximating non-convex surfaces (mainly due to Clarkson) and discuss the main obstruction in establishing a lower bound on the surface. This enables us to give the main conjecture on how to remove the obstruction, which may be used to establish a lower bound. -All the work presented uses intrinsic geometry of surfaces, we exhibit that in general codimension the complexity of an approximation can not depend on the intrinsic geometry of the surface.
This talk introduces the first true vario-scale structure for geographic information: a delta in scale leads to a delta in the map (and smaller scale deltas lead to smaller map deltas until and including the infinitesimal small delta) for all scales. The structure is called smooth tGAP and its integrated 2D space and scale representation is stored as a single 3D data structure: space-scale cube (SSC). The polygonal area objects are mapped to polyhedral representations in the smooth tGAP structure. The polyhedral primitive is integrating all scale representations of a single 2D area object. Together all polyhedral primitives form a partition of the space-scale cube: no gaps and no overlaps (in space or scale). Obtaining a single scale map is computing an horizontal slice through the structure. The structure can be used to implement smooth zoom in an animation or morphing style. The structure can also be used for mixed-scale representation: more detail near to user/viewer, less detail further away by taking non-horizontal slices. For all derived representations, slices and smooth-zoom animations, the 2D maps are always perfect planar partitions (even mixed-scales objects fit together and form a planar partition). Perhaps mixed-scale is not very useful for 2D maps, but for 3D computer graphics it is one of the key techniques. Our approach does also work for 3D space and scale integrated in one 4D hypercube.
We introduce a local operation for polygons and subdivisions called an edge-move. Edge-moves do not change the edge orientations present in the input and are thus suitable for iterative simplification or even schematization. Based on edge-moves we present a new efficient method for area- and topology-preserving subdivision simplification. We show how to tailor this generic method towards the specific needs of building wall squaring and urban-area generalization. Our algorithm is guaranteed to make further progress on any subdivision that has two or more faces and/or reflex vertices. Furthermore, our method produces output of high visual quality and is able to generalize maps with approximately 1.8 million edges in a few hours.
Ray intersection graphs are intersection graphs of rays, or halflines, in the plane. We show that any planar graph has an even subdivision whose complement is a ray intersection graph. The construction can be done in polynomial time and implies that finding a maximum clique in a segment intersection graph is NP-hard. This solves a 21-year old open problem posed by Kratochv'il and Neetil.
In games and simulations, virtual characters need to traverse convincing paths through an environment. A navigation mesh is a data structure on which these paths can be planned. For decades, researchers have mainly focused on two-dimensional navigation meshes, because many environments have a 2D footprint. However, realistic environments may also feature staircases, ramps, and other connections. These environments are not two-dimensional, but multi-layered.
We present the first exact and flexible navigation mesh for multi-layered environments, based on the medial axis. For a set of N two-dimensional layers and K connections (line segments), we build the medial axis in O(KN log N) time. We first compute the medial axis of each layer. Then, we iteratively merge these structures around their connections to obtain one medial axis for the entire multi-layered walkable space. We extend it to a navigation mesh that exactly describes the walkable space using O(KN) storage. It supports flexible paths, characters of all sizes, dynamic updates, and local collision avoidance, and it can simulate tens of thousands of characters in real-time.
Directional relations are fundamental to spatial data queries, analysis and reasoning. Consequently there has been a significant amount of effort to determine directional relations between two regions. However, many existing methods do not perform well when the regions are neighboring or intertwined. In this paper we introduce a new model for directional relations which is based on a splitting line separating the two regions in question. We identify essential quality criteria for directional relation models and translate them into measurable properties of a given splitting line. We present an efficient algorithm that computes an optimal splitting line for two regions and perform extensive experiments. Our results show that the splitting line model captures directional relations very well and that it clearly outperforms existing approaches on pairs of neighboring or intertwined regions.
Dinner is at Hemingway. To get there from the DCGD: Take bus 11 and exit at the Janskerk. The restaurant is a one minute walk from there (on the other side of the road).
It is a 15 minute walk back to the Central Station, or alternatively one can take Bus 11 back to the Central Station.